Understanding Standard Scores in Clinical Practice

This post explains standard scores (Z, T, index etc), considers their clinical implications, and discussed potential conversion methods (tables, apps).

Neuropsychological test scores—whether from cognitive tests, personality assessments, or outcome measures—are a key part of neuropsychology. Understanding neuropsychological test scores is subsequently an essential skill for interpreting test results accurately and meaningfully (Brooks et al., 2011).

Raw scores on their own can only tell you so much. They don’t consider important contextual factors like age or education, which often play a significant role in explaining cognitive variation between individuals. By converting raw scores to standard scores (sometimes called derived scores), we gain a common scale for comparison across different tests and patients. That’s why it’s often recommended to standardise raw scores when analysing neuropsychological test results (Crawford, 2013).

The Z Score

Assuming a normal distribution, test metrics have a known mean and standard deviation (SD). For example, the z score, one of the more common forms of standard score, has a mean of 0 and a SD of 1. The process of deriving a z score from a raw score is a straightforward mathematical process requiring (in addition to the raw score) only the mean and SD for a reference sample (Equation 1).

\[ z = \frac{x - \mu}{\sigma} \tag{1}\]

Where \(x\) is the raw score, \(\mu\) is the mean of the normative sample, and = standard deviation of the sample.

Look Up Tables

Although the above formula is fairly straight forward, would be time intensive and potentially error prone for clinicians to have to perform each of these calculations manually. Fortunately, to aid users, test publishers often provide look-up tables within test manuals for convenient conversion between raw and standard scores. Look-up tables are tables that provide pre-computed values for converting between scores; allowing for efficient conversion and reducing the potential for human error. An example of a look-up table is shown in Table 1.

Table 1: An example of a cognitive test score look-up table.

Raw Score	Z Score	Percentile Rank
15	3.00	>99.9
14	2.67	99.6
13	2.33	98.9
12	2.00	97.7
11	1.67	95.2
10	1.33	90.9
9	1.00	84.1
8	0.67	74.9
7	0.33	63.5
6	0.00	50.0
5	-0.33	36.5
4	-0.67	25.1
3	-1.00	15.9
2	-1.33	9.1
1	-1.67	4.8

Alternatives

In terms of other standard scores, there are many alternatives to the z score (e.g., t, scaled, index). These alternative metrics are available using a small extension of the formula above. This is done by adding the SD of the new metric. (e.g., for a \(T\) score, 10) to the z score, before multiplying this by the mean of the new metric (e.g., for a \(T\) = 50). This formula allows for conversion to a large number of existing alternative standard scores; or, if one is feeling particularly adventurous 🙃, then you can develop your own, by substituting any alternative values for the mean and SD. The mean and SD for a number of common standard scores are shown in Table 2.

Table 2: Details about common standardised scores. Based on Crawford (2013) in L. H. Goldstein (2013). Clinical Neuropsychology: A Practical Guide to Assessment and Management for Clinicians, Second Edition.

Metric	Mean	SD	One unit in SDs	Critique
Index Scores	100	15	0.125	Commonly used, intuitive, but may lack granularity
T Scores	50	10	0.1	Accessible for comparisons; moderate granularity
Z Score	0	1	1.0	Precise but less familiar to non-professionals
Scaled Scores	10	3	0.333	Coarse; adequate for broad interpretations but less detailed
Sten Scores	5.5	2	0.5	Coarse; limited in fine distinctions
Stanine Scores	5	2	0.5	Coarse; limited in fine distinctions
Percentile Ranks	—	—	Varies	Intuitive for non-professionals, but non-linear.

Index Scores

Index scores are among the more commonly used metrics, particularly in clinical settings, and are largely synonymous with the Wechsler family of cognitive tests (e.g., WISC-V, WPPSI-IV, WAIS-IV, WMS-V, etc.). They have a mean of 100 and a standard deviation (SD) of 15, which provides a scale which is intuitive for making comparisons. However, while index scores are helpful for summarising test results, they can lack the finer granularity needed for highly detailed comparisons.

It has also been suggested that index scores have come to be viewed as somewhat pejorative due to their association with the historical context of intelligence testing. However, it is unusual to direct this criticism at a statistical metric; rather, it is more likely a reflection of the contexts in which people have chosen to apply them.

T Scores

T scores are another widely used metric; with a mean of 50 and a standard deviation (SD) of 10, they offer moderate granularity, making them accessible for comparative purposes across various tests. T scores have been applied to many commonly used cognitive assessments, including the Rey-Osterrieth Complex Figure (ROCF), and California Verbal Learning Test, Third Edition (CVLT-III), among others.

Z Scores

Z scores, which have a mean of 0 and a standard deviation (SD) of 1, provide precise, standardised interpretations that are valuable for making comparisons. However, they are often less familiar to non-professionals, which may limit their practical application in broader clinical settings. Given the neuropsychologist’s role in disseminating test scores, it is unlikely that using Z scores will be accessible to clients and referrers.

Scaled Scores

Scaled scores (mean of 10, SD of 3) are often used for subtest-level interpretations in test batteries. Although these scores are generally adequate, their relatively coarse increments can limit comparisons.

Sten and Stanine Scores

Sten scores and Stanine scores both simplify results into easily interpretable scales, although they differ in their average values. Sten scores have a mean of 5.5 and Stanine scores have a mean of 5; while both scales share a standard deviation (SD) of 2. This means that each unit on these scales represents half a standard deviation. This resulting trade-off for simplicity may be viewed as too coarse, particularly when precision is necessary for detailed interpretations.

Percentile Ranks

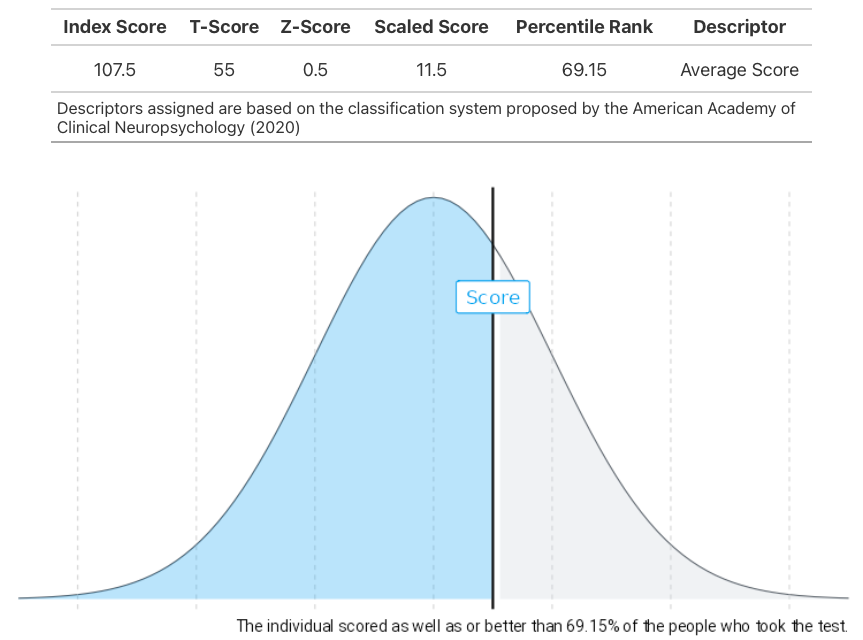
Percentile ranks offer a unique perspective in neuropsychological testing. Unlike traditional standard scores, they utilise a non-linear scale to indicate the percentage of a reference sample or population expected to fall below a given score. For instance, a percentile rank of 85 means the individual performed better than 85% of the reference group, making it an intuitive metric for clients and stakeholders.

However, percentile ranks can lack precision, especially at the extremes of the scoring distribution, where large gaps between scores may reflect minimal differences in performance. While converting standard scores to percentiles is common practice, caution is advised when converting from percentiles to standard scores, unless it is known that the normative data is normally distributed.

Given their relevance, percentile ranks certainly warrant a future post of their own!

Converting Standard Scores

As can be gathered from the previous section, there are many established derived scores, and the range continues to grow as new scores can be easily created¹. Arguments over which is the best metric are somewhat irrelevant, as each can be more or less suitable depending on the situation². The reasons test publishers vary in the metrics included with test manuals can be attributed to several factors, including the target audience, the purpose of the assessment, and the composition of the normative data. This variation highlights the importance of clinicians being knowledgeable about the various metrics available and the contexts in which they are most appropriately applied.

One of the challenges of working with multiple types of standard score is that it requires clinicians to hold frameworks of relative positions for multiple standard scores at once. For example, the discrepency between a z score of 0.22 and a standard score of 104 is far more challenging than if they were both on the same metric. It can therefore be advantageous to have all scores on a consistent metric to aid analysis of test scores. Fortunately, standardised scores can be easily converted among one another. If the z score is available then Equation 1 can be applied, otherwise Equation 2.

\[ X_{new} = \frac{s_{new}}{s_{old}} (X_{old} - \bar{X}_{old}) + \bar{X}_{new} \tag{2}\]

Where \(X_{new}\) is the newly converted (or derived) score, \(s_{new}\) and \(s_{old}\) refer to the SD value for both new and old metrics, \(\bar{X}_{new}\) and \(\bar{X}_{old}\) are the mean value for the new and old metrics, and finally \(X_{old}\) is the original standard score.

Conversion Tables

Similarly, clinicians can use a standard score conversion table to avoid the need to convert scores manually. This is simply another form of look up table for converting between standard scores (exclusive of raw scores). Many versions of these are freely available in neuropsychology textbooks or on the internet (for an example see Table 3).

Standard score conversion tables are popular for their convenience in converting among scores and adopting a single metric. It is otherwise challenging to judge the discrepancy between scores (for example, a z score of 0.32 and a standard score of 104) as this requires clinicians to hold frameworks of relative positions for multiple standard scores at once.

Table 3: Example segment of a neuropsychology conversion table.

Index Score	Percentile Rank	Scaled Score	T Score	Z Score	Descriptor
150	>99.9	—	—	—	Very Superior
149	>99.9	—	—	—	Very Superior
148	99.9	—	—	—	Very Superior
147	99.9	—	—	—	Very Superior
146	99.9	—	—	—	Very Superior
145	99.9	19	80	+3.00	Very Superior
144	99.8	—	—	—	Very Superior
143	99.8	—	—	—	Very Superior
142	99.7	—	78	+2.75	Very Superior
141	99.7	—	—	—	Very Superior
140	99.6	18	77	+2.67	Very Superior
139	99.5	—	—	—	Very Superior
138	99	—	—	—	Very Superior
137	99	—	75	+2.50	Very Superior
136	99	—	—	—	Very Superior
135	99	17	73	+2.33	Very Superior
134	99	—	—	—	Very Superior
133	99	—	72	+2.25	Very Superior
132	98	—	—	—	Very Superior
131	98	—	—	—	Very Superior
130	98	16	70	+2.00	Very Superior
129	97	—	—	—	Superior
128	97	—	68	+1.75	Superior
127	96	—	—	—	Superior
126	96	—	—	—	Superior
125	95	15	67	+1.67	Superior
124	95	—	—	—	Superior
123	94	—	65	+1.50	Superior
122	93	—	—	—	Superior
121	92	—	—	—	Superior

Problems with Conversion Tables

While standard score conversion tables are popular tools in neuropsychology, they do come with some significant drawbacks.

For starters, converting scores using these tables is a manual process. This task might seem quick when you’re dealing with just a few tests, but it can become quite time-consuming when working with larger test batteries. It’s important to note that even a small delay can add up, especially since clinicians often conduct multiple assessments regularly. The cumulative time spent flipping through tables can detract from valuable time that could be spent on analysis and patient care.

Another limitation of standard score conversion tables is that they don’t provide every possible value for more granular metrics (such as z scores). To keep these tables manageable, authors often only include fixed increments—like 0.125 for z scores. This can lead to a loss of precision because not all combinations of scores are represented. For example, if you need to convert a z score of 2.20 to an index score (such as in Table 1), you might find there’s no exact match available.

When faced with this matching issue, clinicians have a few options. They could:

1. Report a range of adjacent values (like saying a z score of 2.20 corresponds to an index of 130-133)

2. Make an educated guess based on the nearest value (perhaps estimating it at 132)

3. Round down to the nearest available score (which might lead to an index of 130)

4. Manually calculate the score using a formula.

While the first three options can compromise precision, using a formula will give the most accurate result (in this case, an index of 133). However, despite the relative simplicity of the math involved, using this method can still increase the risk of human error and time to perform due.

Finally, it is worth noting that when using a formula, it becomes clear that many of the values in common look up tables are imprecise, and with different rounding conventions³.

For the reasons outlined above, it can be helpful to use an electronic scoring tools, such as a purpose developed spreadsheet or web application. The NeuroPsyTools app Score Converter is one example of a web application that can automate this process.

Screenshot of the web app Score Converter, demonstrating an electronic tool for converting test scores.

Summary

Standardising raw test scores is often an essential part of many neuropsychological assessment. Choosing the right type of standard score depends on the context, and understanding these options can make all the difference to picking the best option. We’ve covered the key formulas for converting between standard scores and explored the best ways to handle these conversions—whether by manual calculation, using lookup tables, or leveraging web calculators.

References

Brooks, B. L., Sherman, E. M. S., Iverson, G. L., Slick, D. J., & Strauss, E. (2011). Psychometric Foundations for the Interpretation of Neuropsychological Test Results (M. R. Schoenberg & J. G. Scott, Eds.; pp. 893–922). Springer US. https://doi.org/10.1007/978-0-387-76978-3_31

Crawford, J. R. (2013). Quantitative Aspects of Neuropsychological Assessment (L. H. Goldstein & J. E. McNeil, Eds.; 2nd ed). Wiley-Blackwell.

Footnotes

1. One known example to the authors includes Vineland scaled scores (M = 15, SD = 3).

2. See (Crawford, 2013) for a more detailed discussion.

3. For example, Table 1 shows that the index score equivalent of z = 2.25 would be 1.33, however when using a formula with 2 decimal places the value provided is 133.75.